Grigori Perelman

Grigori Perelman is an interesting mathematician who almost does not communicate with other mathematicians and at the same time has solved difficult problems in the field of geometry. STUDY AREA and SUBJECTS The subject of the work is the eminent Leningrad mathematician Grigori Perelman, born on June 13, 1966 Perelman is presently a victim of acute lonersy, which is added to the mystery of his great achievements in mathematics.

Perelman’s pedagogical education can be explained by his gift in mathematics since childhood that brought him to the specialized education and Leningrad State University. This period could be considered as the young age achievement in academic career, as he received the doctorate at the age of 24.

In 2000s, he expanded knowledge in topology by providing solution for the Poincaré conjecture, which has been titled as one of the Clay Institute’s seven millennium problems since 1904. This difficult and fine problem, solved thanks to the idea of the theory of Ricci flow developed by Richard S. Hamilton, made him renowned on the international level.

Perelman turned down many awards; he did not collect the Fields Medal and Clay Millennium Prize, either. He decided to retreat from the spotlight and stop writing for the public in an effort to establish a personal life as well as engaging in mathematics for other interests.

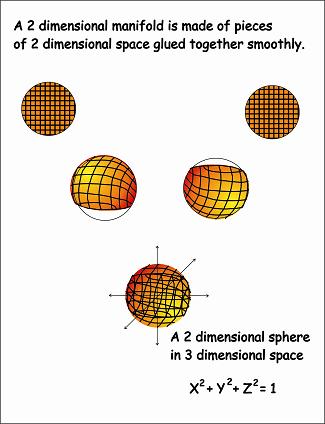
Although some of the ideas of Perelman relate close to the area of topology, his proof for the Poincaré conjecture is remarkable and will always remain the part of the great achievements of the mathematicians. His decisions, especially his absence from the public raised many questions about him, however, his impact continues to be felt. His works have remained relevant in geometry together with topology, an indicator that he had a very particular contribution towards the development of mathematics.

Perelman’s story is another account of the calculation of valedictory mathematics and individual liberty: the quest for satisfactory realization of one’s intellectual capacity free from interference. His work will always encourage future generations to look deeper into the endless and complex world of mathematical conception.